Subcircuits

Several circuits or systems of practical interest involve a large number of blocks (elements). In such cases, the schematic diagram can be significantly simplified using subcircuits (hierarchical blocks). In this section, we will first explain how a simple subcircuit can be designed using the schematic capture GUI. We will then look at more complex subcircuits, including an induction motor model.

Some comments about sub-circuit files are in order. As described in the section on Getting started, the GSEIM distribution already has several sub-circuits, and the concerned files are located in the $SUBCKT and $SUBCKT_GRC directories. These sub-circuits can be used by the user in a new circuit (project). In addition, the user can make up new sub-circuits. A sub-circuit named sub1, for example, involves three files:

  • sub1.grc : This file describes the schematic diagram of the sub-circuit prepared by the user.
  • sub1.hblock.yml : This file is generated when the user opens sub1.grc in the GUI and clicks on the Generate circuit file button in the menu bar.
  • sub1_parm.py : This is a python file, to be written by the user, if the sub-circuit involves computed parameters, i.e., parameters whose values need to be computed.

Of these three files, sub1.grc can be saved by the user in a directory of their choice. The path of the other two files is given by the value assigned to the variable HIER_BLOCK_USER_DIR while invoking GSEIM. For example, if the user wants to use ~/subckt_dir for saving sub1.hblock.yml and sub1_parm.py, then the commands to invoke GSEIM (see Installation Instructions) should be modified as follows.

  • Pre-built image:

    HIER_BLOCK_USER_DIR=~/subckt_dir/ gseim-gui

  • Building from source:

    HIER_BLOCK_USER_DIR=~/subckt_dir/ bazel run //grc:gseim_gui

In the following, we will denote the value assigned to HIER_BLOCK_USER_DIR by $HIER_BLOCK_USER_DIR. With this background, we can now discuss a few specific sub-circuits.

Linear transformation

Let us see how to make up a subcircuit to implement the linear transformation given by,

(38)\[\begin{split}\left[ \begin{array}{c} y_1 \\ y_2 \end{array} \right] = \left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right] \thinspace \left[ \begin{array}{c} x_1 \\ x_2 \end{array} \right] \,,\end{split}\]

where \(x_1\), \(x_2\) are the input nodes (variables), and \(y_1\), \(y_2\) are the output nodes. Eq. (38) can be implemented as follows.

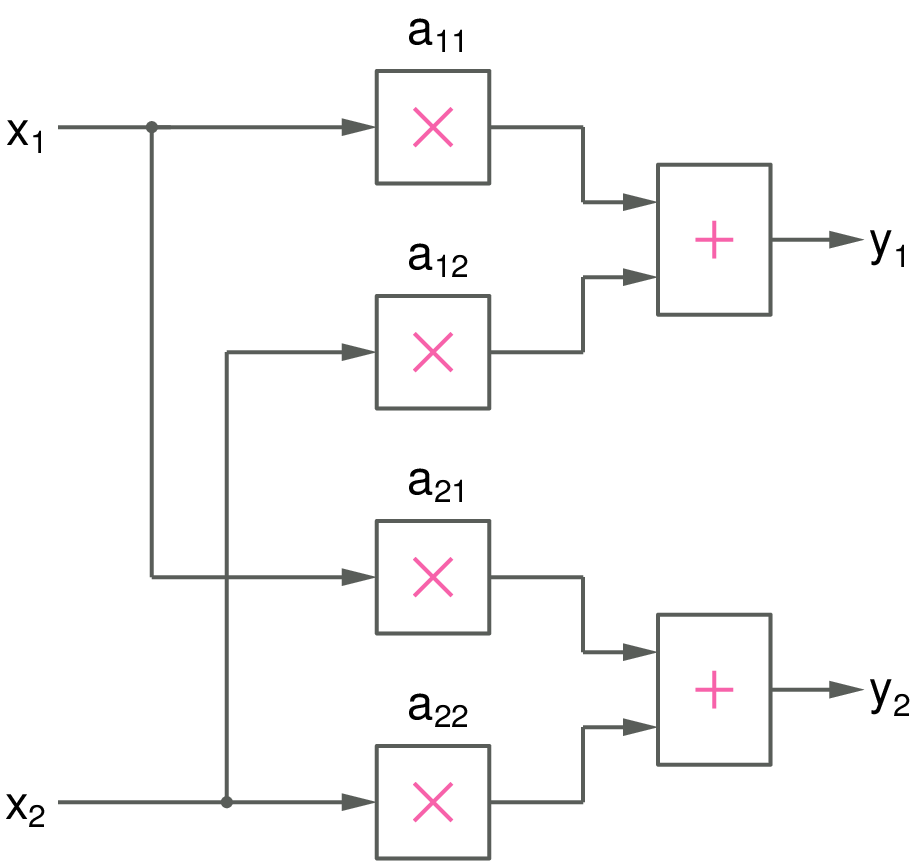
subckt example

To convert this block diagram into a GSEIM subcircuit, we can use the step-by-step procedure given below.

  • Start a new project. A canvas with an Options block will appear. Double-click on the options block, and set Id and Title. Note that Id should only contain letters, digits, and the underscore character. As a convention, it is a good idea to start Id with s_ (s for subcircuit); however, it is not really required. In the Generate option field, choose Hier Block to indicate that this schematic diagram is for a hierarchical block (subcircuit) and not a stand-alone system.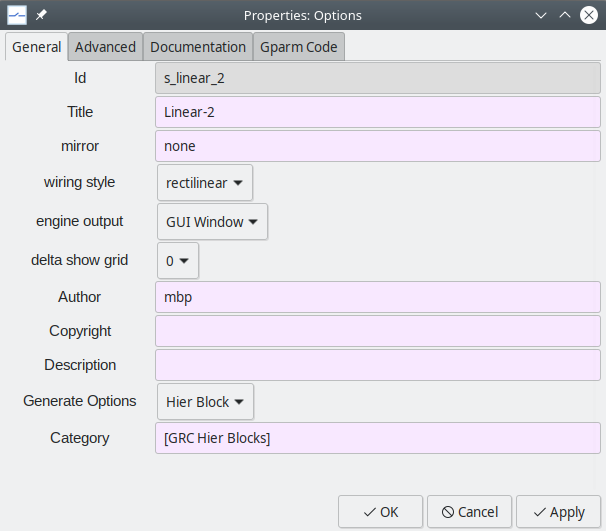

    options block

  • Save the subcircuit schematic. It is a good practice to use a file name which reflects the name (Id) of the subcircuit. In our example, it would be s_linear_2.grc. Save s_linear_2.grc in a suitable directory.

  • The next step is to bring in the required elements (blocks) from the library (see Creating a new project). We need four multscl (multiply by scalar) elements and two sum_2 elements. Place the components, keeping in mind the connections we need to make.

    placement of blocks

  • Next, we need to provide pads for our subcircuit. We need two source pads (for \(x_1\) and \(x_2\)) and two sink pads (for \(y_1\) and \(y_2\)). The source pads will show up as input pads when we invoke this subcircuit from a higher level; similarly, the sink pads will show up as output pads. Bring in the source and sink pads from the block tree panel \(\rightarrow\) Misc \(\rightarrow\) subcircuit pads.

  • Double-click on each of the source and sink pads and name those as x1, x2, y1, y2. Assign x1 to the source pad which you brought in first, and x2 to the one you brought in later. Similarly, name the sink pad you brought in first as y1 and the other sink pad as y2. When this procedure is followed, the subcircuit, when invoked, will have the order x1, x2 for the input nodes (ports), and y1, y2 for the output nodes.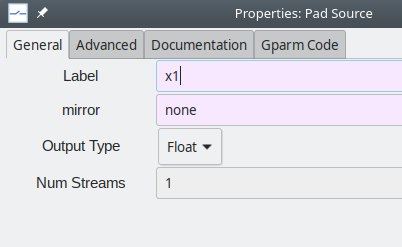

    pad properties

  • Bring in two connectors, connector_f_3a and connector_f_3b, and place them suitably. Your schematic should now look like this: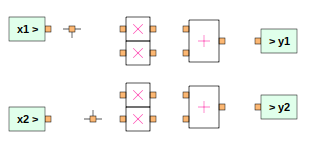

    schematic 1

  • Connect the elements as required. To make a connection between two ports, click on one of the ports and then the other.

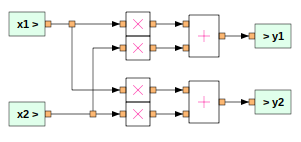
    schematic 2

  • Our next step is to assign the multiplier parameter (k) of each multscl element the values shown below.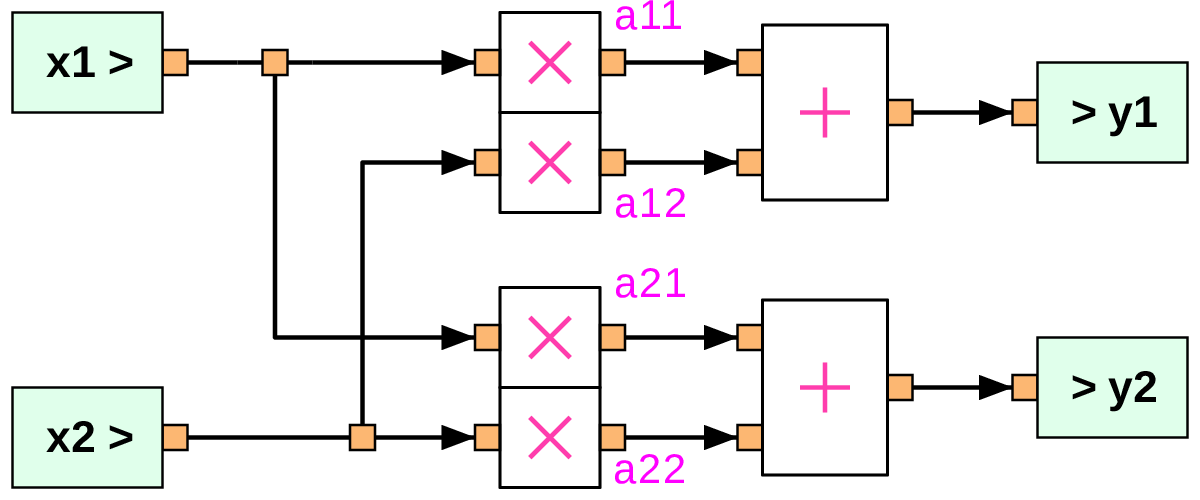

    multscl parameters

  • Note that we will need to make a11, a12, a21, a22 assignable when this subcircuit is invoked. This is achieved with the help of global parameters. Click on GParms \(\rightarrow\) Add gparm, and change the name as shown below.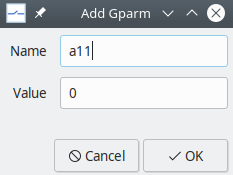

    add gparm

    Repeat for a12, a21, a22.

  • We now map the global parameters to the k parameters of the multscl elements. Double-click on the top multscl element in the schematic and assign a11 to k. Similarly, make suitable assignments for the other three multscl elements.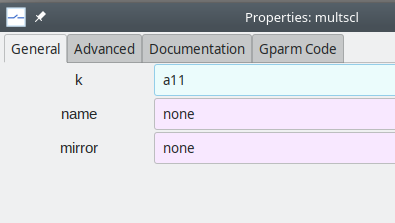

    assignment of a11

  • Click on Generate circuit file. This creates a file $HIER_BLOCK_USER_DIR/s_linear_2.hblock.yml, a text file which can be opened with a text editor such as vim, emacs, gedit. Notice that the .grc file to which we have saved the schematic appears in the grc_source field in s_linear_2.hblock.yml.

    End your GSEIM session and start it again. You will find the newly added subcircuit listed under GRC Hier Blocks. Note that the label which appears in this list (s_linear_2) corresponds to the Id value we entered in the Options block earlier.

  • Drag and drop the subcircuit into the canvas.

    Hovering over a port displays the name of that port. By convention, ports corresponding to pad_source blocks in the subcircuit schematic (x1 and x2 in our case) appear on the left of the subcircuit symbol, and those corresponding to pad_sink blocks (y1 and y2 in our case) appear on the right, as shown below.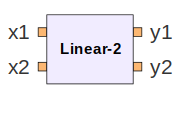

    subckt symbol

  • Double-clicking on the subcircuit opens the following dialog box, enabling the user to edit the parameter values as required.

    Alternative text

Induction motor

We now consider the induction motor model described in Element Templates. The model equations are reproduced below.

(39)\[\displaystyle\frac{d{\psi}_{ds}}{dt} = v_{ds}-r_si_{ds},\]
(40)\[\displaystyle\frac{d{\psi}_{qs}}{dt} = v_{qs}-r_si_{qs},\]
(41)\[\displaystyle\frac{d{\psi}_{dr}}{dt} = -\,\frac{P}{2}\,\omega_ {rm}\psi _{qr}-r_ri_{dr},\]
(42)\[\displaystyle\frac{d{\psi}_{qr}}{dt} = \frac{P}{2}\,\omega_ {rm}\psi _{dr}-r_ri_{qr},\]
(43)\[\displaystyle\frac{d{\omega}_{rm}}{dt} = \frac{1}{J}\,(T_{em}-T_L),\]

where

(44)\[i_{ds} = \frac{L_r}{L_m L_e}\,\psi _{ds} - \frac{1}{L_e}\,\psi _{dr},\]
(45)\[i_{qs} = \frac{L_r}{L_m L_e}\,\psi _{qs} - \frac{1}{L_e}\,\psi _{qr},\]
(46)\[i_{dr} = \frac{1}{L_m}\,\psi _{ds} - \left(\frac{L_{ls}}{L_m}+1\right)~i _{ds},\]
(47)\[i_{qr} = \frac{1}{L_m}\,\psi _{qs} - \left(\frac{L_{ls}}{L_m}+1\right)~i _{qs},\]
(48)\[T_{em} = \frac{3}{4}\, P L_m\,(i_{qs}i_{dr} - i_{ds}i_{qr}),\]

with

(49)\[L_e = \displaystyle\frac{L_sL_r}{L_m}-L_m,\]
(50)\[L_s = L_{ls}+L_m,\]
(51)\[L_r = L_{lr}+L_m.\]

We first rewrite Eqs. (39) to (43) such that each of them can be implemented using basic blocks such as adder, multiplier, integrator, etc.

As an example, Eq. (41) can be rewritten as,

(52)\[\psi _{dr} = \int \left(-\,\frac{P}{2}\,\omega _{rm}\psi _{qr}-r_r i_{dr}\right)\,dt,\]

which can be implemented using the mult_2 element (to multiply \(\omega _{rm}\) and \(\psi _{qr}\)), and the sum\_2 and integrator elements described in Element Templates. Treating Eqs. (39) to (43) in this manner, we obtain the subciruit shown below (the .grc file is ~/gseim_grc/subckt_grc/s_indmc.grc).

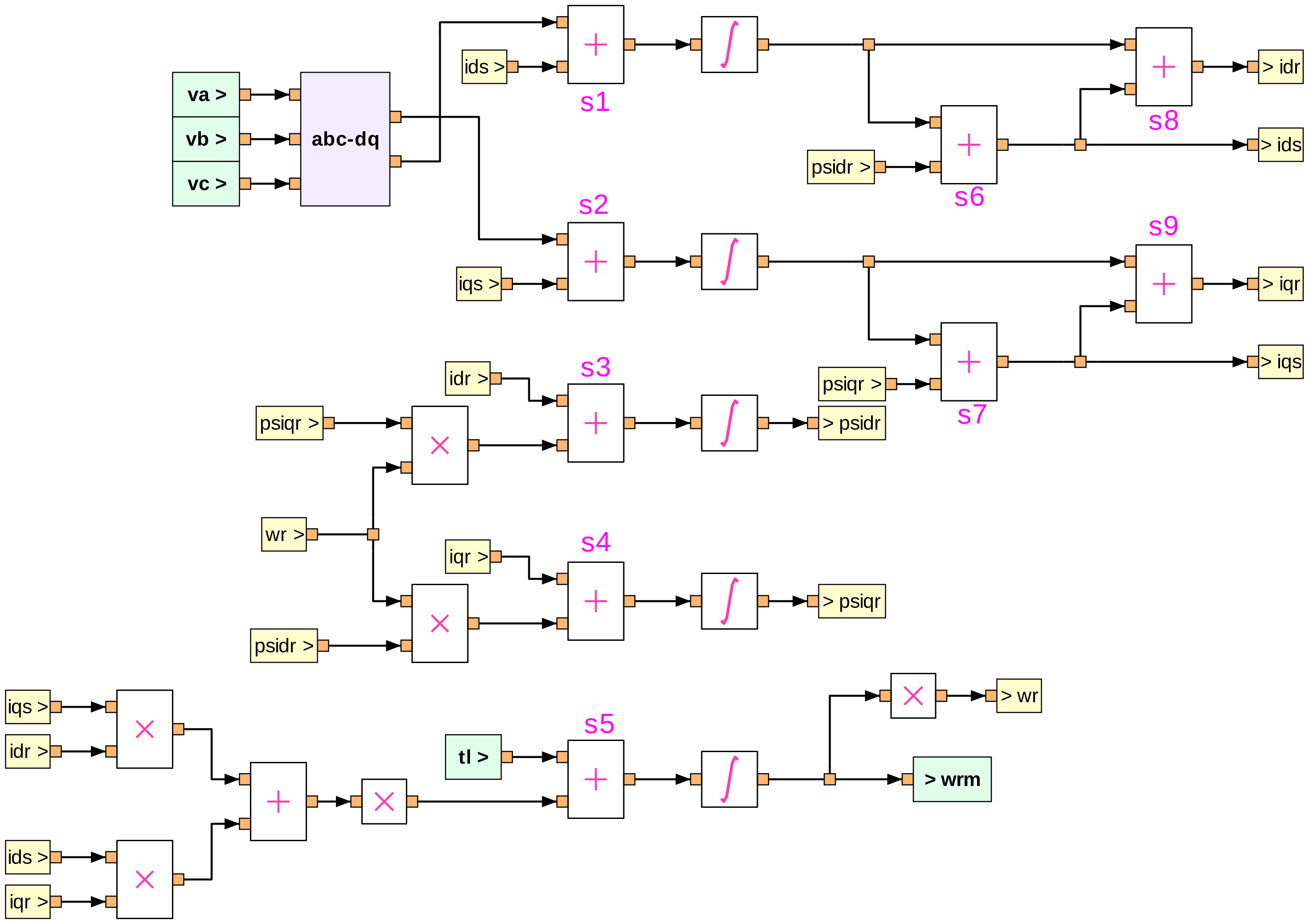
indmc subcircuit

The following additional points about the implementation may be noted:

  • Virtual (dummy) sources and sinks (shown in light yellow colour) are used in order to make wiring less cumbersome. For example, note the virtual sink marked >idr and the virtual source marked idr>, the two corresponding to the same node.

  • Input and output pads (shown in light green colour) are used to indicate the input and output ports of the subcircuit symbol when it is invoked from a higher level. For the induction machine subcircuit, va, vb, vc, tl are the input ports, and wrm is the output port. When the subcircuit is invoked, the input ports appear on the left, and the output ports on the right, as shown below.

    indmc symbol

  • The subcircuit has the following parameters: j, llr, lls, lm, poles, rr, rs, which correspond to \(J\), \(L_{lr}\), \(L_{ls}\), \(L_m\), \(P\), \(r_r\), \(r_s\), respectively, in Eqs. (39) to (43). In implementing the equations, we need to compute quantities which depend on these parameters. For example, consider Eq. (44) for \(i_{ds}\), implemented using the sum\_2 element marked as s6 in the figure. This element gives

    \[i_{ds} = k_1\psi _{ds} + k_2\psi _{dr},\]

    which requires \(k_1 = \displaystyle\frac{L_r}{L_mL_e}\), \(k_2 = -\,\displaystyle\frac{1}{L_e}\) to be assigned. For all such assignments, the user is expected to supply a python file specific to the concerned subcircuit, and it needs to be in the same directory as the .yml file for that subcircuit. For s_indmc, the python file is ~/gseim_grc/subckt/s_indmc_parm.py, and is reproduced below.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
    def s_indmc_parm(dict1):

    j     = float(dict1['j'    ])
    llr   = float(dict1['llr'  ])
    lls   = float(dict1['lls'  ])
    lm    = float(dict1['lm'   ])
    rr    = float(dict1['rr'   ])
    rs    = float(dict1['rs'   ])
    poles = float(dict1['poles'])

    ls = lls + lm
    lr = llr + lm
    le = (ls*lr/lm) - lm
    l1 = lr/(lm*le)
    l2 = 1.0 + (lls/lm)
    l3 = lls/lm
    x1 = 0.75*poles*lm
    x2 = 0.5*poles

    i1_k = 1.0/j

    s1_k1 = 1.0
    s1_k2 = -rs

    s2_k1 = 1.0
    s2_k2 = -rs

    s3_k1 = -rr
    s3_k2 = -1.0

    s4_k1 = -rr
    s4_k2 =  1.0

    s6_k1 = l1
    s6_k2 = -1.0/le

    s7_k1 = l1
    s7_k2 = -1.0/le

    s8_k1 = 1.0/lm
    s8_k2 = -l2

    s9_k1 = 1.0/lm
    s9_k2 = -l2

    m1_k = x1

    dict1['i1_k' ] = '%14.7e' % (i1_k )
    dict1['s1_k1'] = '%14.7e' % (s1_k1)
    dict1['s1_k2'] = '%14.7e' % (s1_k2)
    dict1['s2_k1'] = '%14.7e' % (s2_k1)
    dict1['s2_k2'] = '%14.7e' % (s2_k2)
    dict1['s3_k1'] = '%14.7e' % (s3_k1)
    dict1['s3_k2'] = '%14.7e' % (s3_k2)
    dict1['s4_k1'] = '%14.7e' % (s4_k1)
    dict1['s4_k2'] = '%14.7e' % (s4_k2)
    dict1['s6_k1'] = '%14.7e' % (s6_k1)
    dict1['s6_k2'] = '%14.7e' % (s6_k2)
    dict1['s7_k1'] = '%14.7e' % (s7_k1)
    dict1['s7_k2'] = '%14.7e' % (s7_k2)
    dict1['s8_k1'] = '%14.7e' % (s8_k1)
    dict1['s8_k2'] = '%14.7e' % (s8_k2)
    dict1['s9_k1'] = '%14.7e' % (s9_k1)
    dict1['s9_k2'] = '%14.7e' % (s9_k2)
    dict1['m1_k' ] = '%14.7e' % (m1_k )
    dict1['x2'   ] = '%14.7e' % (x2   )

    The k1 and k2 values for the sum_2 element marked as s6 in the schematic are computed in the above python function as s6_k1 and s6_k2, respectively. At the end of the function, all of these computed values are stored in the parameter dictionary for this subcircuit. With this mechanism, the user has significant flexibility in implementing element equations.

  • The user can define output parameters for a subcircuit and use those at higher levels. The output parameters can be mapped to nodes within the subcircuit or to the output parameters of the blocks involved in the subcircuit. These features provide a mechanism for viewing various quantities of interest at different levels when the system is simulated.

Voltage source inverter

Next, we consider a subcircuit with electrical elements, viz., a three-phase voltage source inverter. The GSEIM implementation is shown below.

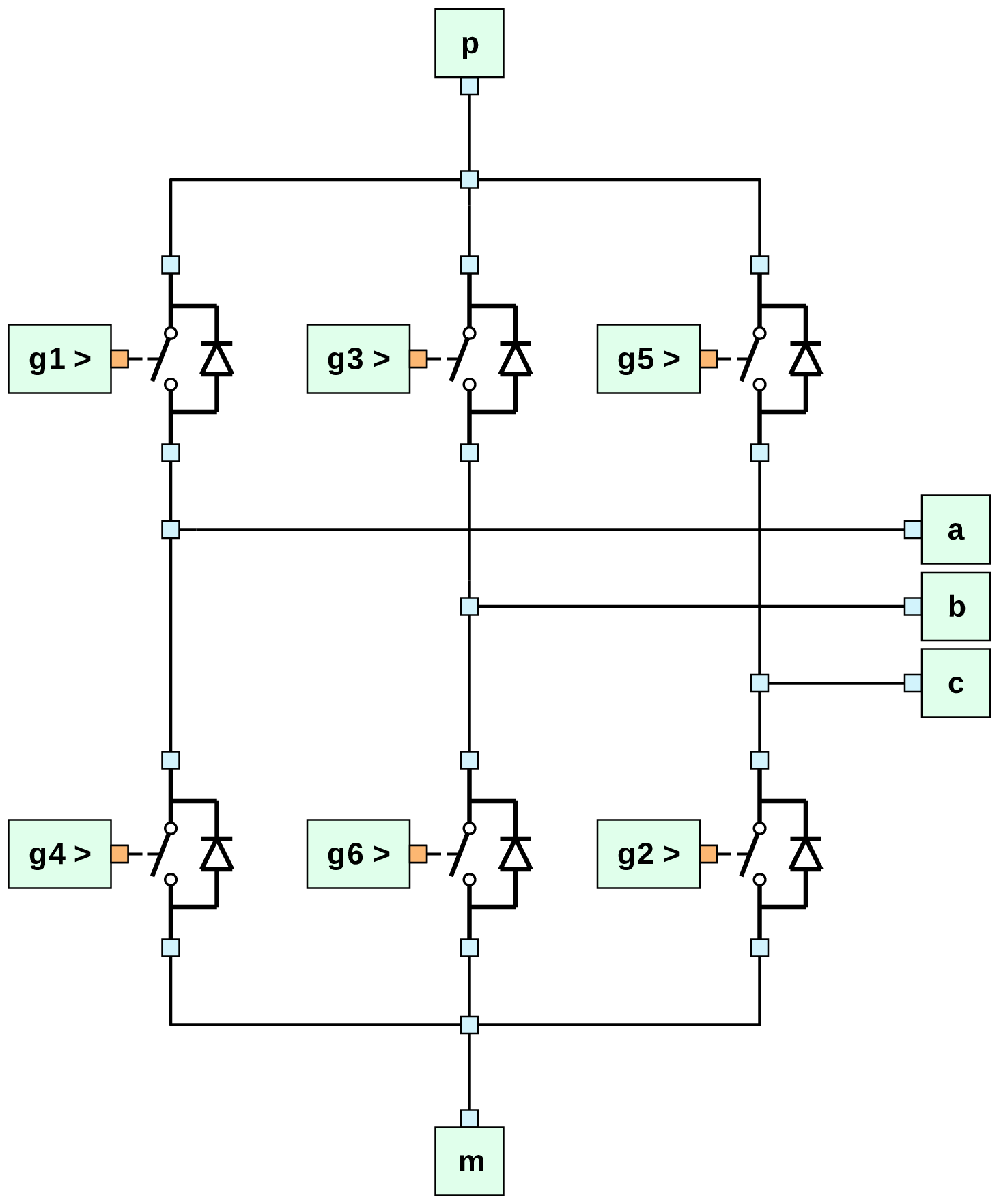
three-phase VSI

When the subcircuit is called from a higher level, it appears as follows.

VSI symbol